ECUACIONES LINEALES

                                        
http://noticias.universia.edu.pe/net/images/educacion/c/cu/cur/curso-online-gratuito-de-algebra.jpg

PRESENTACIÓN 
El  presente trabajo estará dirigido al área educativa.  En el cual se mostraran  temas relacionados a las  ecuaciones lineales con el  fin de compartir conocimiento ,mostrar de una manera sencilla y didáctica la ejecución a ejercicios relacionados a su especialidad. Asimismo este blog cuenta con información objetiva y verídica de fuentes como libros de Salvador Timoteo . Razonamiento Matemático. y Haeussler Ernest. Matemáticas para administración y economía. Así como también de fuentes seguras sacadas de Internet.

OBJETIVOS

-      Opinar

–       Enseñar

–       Colaborar

–       Contribuir

–       Intercambio de información

–       Compartir conocimiento

–       Transformar el conocimiento

–       Transformar las actitudes y aptitudes de los estudiantes,

–       Y, estudio colaborativo en todos los niveles, etc.

TEMAS

1. ¿QUÉ ES UNA ECUACIÓN LINEAL?
2. PARTES DE UNA ECUACIÓN LINEAL
3. TIPOS DE ECUACIONES LINEALES
4. PLANTEO DE ECUACIONES
5. PROBLEMAS DE APLICACIÓN RELACIONADOS A SU ESPECIALIDAD

               ¿QUÉ ES UNA ECUACIÓN LINEAL?

Una ecuación lineal en la variable x es una ecuación que puede escribirse en la forma ax+b=O, en donde a y b son constantes y a # O. 
     FUENTE: Haeussler Ernest. Matemáticas para administración y economía 2º edición .ed.Pearson.Pag 35

EJEMPLOS:

FUENTE: Haeussler Ernest. Matemáticas para administración y economía 2º edición .ed.Pearson.Pag 35-46

                    

FUENTE: Haeussler Ernest. Matemáticas para administración y economía 2º edición .ed.Pearson.Pag 35-46

FUENTE: Haeussler Ernest. Matemáticas para administración y economía 2º edición .ed.Pearson.Pag 35-46

PARTES DE UNA ECUACIÓN LINEAL

Cada Ecuación Lineal tiene elementos que le son propios:

• Una a más variables que se abrevian mediante letras, y que representan cantidades desconocidas;
• Todas las variables están elevadas a la primera potencia, y sin multiplicarse entre sí;
• Se establece una igualdad. Es decir, se trata de una proposición que indica que una cantidad es igual a otra.

Ejemplos de ecuaciones que son:
	lineales
	no lineales

	x + 3 = 5
	x + y = 2
	x2 + y = 3
	x + y + z = 0,5
	x + z2 – xz = 9

FUENTE:http://ww2.educarchile.cl/portal.herramientas/sitios_educativos/EcuacionesLineales/sitio/elementos.htm

 TIPOS DE ECUACIONES LINEALES

las ecuaciones se pueden clasificar en tres tipos dependiendo de su conjunto de soluciones:

Ecuación condicional

Suponga que se tiene una igualdad con una variable. Si la igualdad se cumple para algunos valores de la variable y para otros no, se llama una ecuación condicional.

  

Ejemplo: 

x + 2 = 0 es una ecuación condicional pues se tiene al menos un valor de la variable que es solución: x = –2 y hay otros valores de la variable que no son solución: x = –1 no es solución 

Fuente:http://www.matematicatuya.com/NIVELACION/ECUACIONES/S1identidad.html

Ecuación de identidad

Una igualdad que se cumple para cualquier valor permitido de la variable se denomina una identidad.

Ejemplo:

  

  ( x –1)² – 1= x( x – 2)   es una identidad
Para demostrarlo, nosotros partiremos del lado izquierdo, aplicaremos propiedades, e identidades hasta llegar al lado derecho.     = x² – 2x + 1 – 1     producto notable     = x² – 2x     factorizamos
    = x( x – 2)

Fuente:http://www.matematicatuya.com/NIVELACION/ECUACIONES/S1identidad.html

Ecuación de una contradicción

Una ecuación es una contradicción si no tiene solución. Es decir, si no hay ningún valor dela variable que haga cierta la igualdad.

Ejemplo:

x² + 1 = 0   es una contradicción Una manera de demostrarlo es argumentando que el miembro izquierdo es mayor a cero para cualquier valor de la variable. Así no hay un valor posible de la variable que haga cierta la igualdad.

Fuente:http://www.matematicatuya.com/NIVELACION/ECUACIONES/S1identidad.html

PLANTEO DE ECUACIONES

Fuente:Salvador Timoteo.Razonamiento Matematico.2ºedición .ED.San Marco.pag 195-220

Ejemplos:

1.Marta tiene 15 años, que es la tercera parte de la edad de su madre. ¿Qué edad tiene la madre de Marta?

Llamamos x a la edad de la madre.

La tercera parte de la edad de la madre es la misma que la de Marta, es decir, 15. Escrito matemáticamente:

$$\frac{x}{3}=15$$

Por tanto, la edad de la madre es x = 45.

https://www.matesfacil.com/ESO/Ecuaciones/resueltos-problemas-ecuaciones.html

2.Héctor guarda 25 euros en su hucha, que supone sumar una cuarta parte del dinero que ya había. ¿Cuánto dinero hay en la hucha?

Llamamos x al dinero que había en la hucha

25€ es la cuarta parte de lo que había, es decir,

$$25=\frac{x}{4}$$

La solución de la ecuación es

$$x=25\cdot 4=100$$

Por tanto, en la hucha había 100€ y ahora hay

$$100+25=125euros$$

https://www.matesfacil.com/ESO/Ecuaciones/resueltos-problemas-ecuaciones.html

3.La tercera parte de las cucharas de la casa estaban en el lavaplatos y las restantes en el cajón. Pero la mitad de las cucharas del cajón, 15, se llevan a la mesa. ¿Cuántas cucharas hay en el lavaplatos?

x = cucharas en la casa

En el lavaplatos hay la tercera parte del total, es decir:

$$\frac{x}{3}$$

Las restantes estaban, al principio, en el cajón. Había en el cajón

$$\frac{2x}{3}$$

La mitad de las que había en el cajón son 15 cucharas. Es decir, en el cajón había 30.

Podemos igualar a 30 la expresión anterior:

$$\frac{2x}{3}=30$$

De donde obtenemos que

$$x=\frac{30\cdot 3}{2}=45$$

En la casa hay 45 cucharas. De estas 45 cucharas, 15 están en el lavaplatos. Las 30 restantes están 15 en la mesa y 15 en el cajón.

https://www.matesfacil.com/ESO/Ecuaciones/resueltos-problemas-ecuaciones.html

PROBLEMAS DE APLICACIÓN RELACIONADOS A SU ESPECIALIDAD

1)Letizia y Marta han ido de compras en las rebajas. La primera ha comprado unos pantalones de $42 y una camisa de $24 y, la segunda, un suéter de $28 y unos zapatos de $60.

Después de aplicar los descuentos, Letizia ha pagado $50,4 y Marta, $64,4.

Calcular los porcentajes de descuento aplicados sabiendo que el porcentaje aplicado a los pantalones y al suéter coincidían y el aplicado a la camisa y a los zapatos también.

Antes de resolver el problema vamos a ver un ejemplo de cómo trabajar con descuentos.

Si a un artículo de $40 se le aplica un descuento de 10%, el precio final se corresponde con el 90% del precio inicial. Es decir, el precio final sería el 90% de $40. Para calcular dicho porcentaje realizamos la siguiente operación:

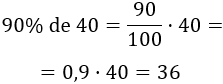
El precio final del artículo sería $36.

Si $x$ representa el porcentaje de descuento, hemos multiplicado el precio inicial por

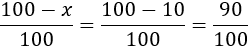
Resolución del problema:

Si el porcentaje de descuento de los pantalones y del suéter es $x$ y el de la camisa y el de los zapatos es $y$, entonces, según lo que hemos dicho, tenemos el sistema de ecuaciones

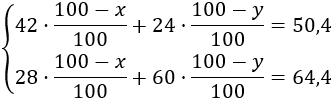
Multiplicamos ambas ecuaciones por 100 para evitar los denominadores:

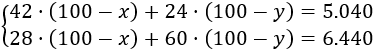
Seguimos operando:

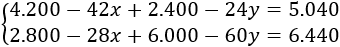
Simplificamos:

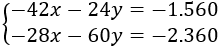
Resolvemos el sisma por reducción. Multiplicamos la primera ecuación por 2/3 para poder eliminar una incógnita al restar las ecuaciones:

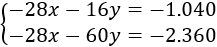
Restamos las ecuaciones:

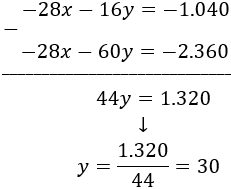
Calculamos $x$ a partir de alguna de las ecuaciones anteriores:

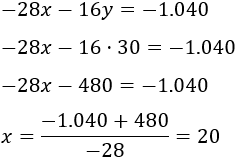
Por tanto, se han aplicado descuentos del 20% y del 30%.

Fuente:https://www.problemasyecuaciones.com/Ecuaciones/problemas/sistemas/problemas-ecuaciones-sistemas-lineales-resueltos-numeros-edades-incognitas-ejemplos-explicados.html

2)Una librería consta de 5400 libros repartidos en tres estancias: en la estancia A hay el triple de libros que en la B y en la B la mitad que en la C. Calcular cuántos libros hay en cada estancia.

Sea x la cantidad de libros en la estancia B.

• En la estancia A hay el triple de libros que en la B, es decir, hay 3x.
• En la estancia B hay la mitad que en la C, que es lo mismo que decir que en C hay el doble que en B, es decir, en C hay 2x.
• Sabemos que en total hay 5400, luego la suma de los libros de todas las estancias es 5400.
  Obtenemos la ecuación:
  
  $$3x+x+2x=5400$$
  Cuya solución es
  
  $$x=\frac{5400}{6}=900$$

Como x representa los libros que hay en B, tenemos:

• La cantidad de libros en B es
  
  $$x=900$$
• La cantidad de libros en A es
  
  $$3x=3\cdot 900=2700$$
• La cantidad de libros en C es
  
  $$2x=2\cdot 900=1800$$

3)

Fuente:Salvador Timoteo.Razonamiento Matematico.2ºedición .ED.San Marco.pag 195-220